Thermal velocities in the plasma of a MOA Device A Brief Summary to an Adiabatic Plasma Heating Process
Manfred Hettmer*
Johann Gottek-Gasse 39, Austria.
*Corresponding Author
Manfred Hettmer,
Johann Gottek-Gasse 39, Austria.
Tel: +43 676 54 020 69
Email: manfred.hettmer@gmail.com
Received: March 02, 2023; Accepted: April 12, 2023; Published: April 27, 2023
Citation:Manfred Hettmer. Thermal velocities in the plasma of a MOA Device. Int J Aeronautics Aerospace Res. 2023;10(1):297-300.
Copyright: Manfred Hettmer© 2023. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
Abstract
Although a privately funded technology is in need for some discretion it also should be scientific discussed. Therefore the
topic of this brief summary is to introduce some results in a little bit more detail rather than technical details of the MOA
thruster. In some settings a MOA device can be adjusted to reach exhaust velocities in the range analog to the targeted temperatures
of nuclear fusion devices. These results are documented by the method of measuring the kinetic impact energy
of ions. Although MOA has the ability to generate fusion temperatures in the ion gas of a plasma but the system is not
designed to generate reaction rates necessary to realize a positive energy balance. If the principle of its heating mechanism
has the capability of a fusion device it may be recognized in future developments and this idea is not affecting the current
development yet. At the moment the technique should be optimized for applications which to perform it is able now. But
some results are worthy to be discussed in the view of extended applications in possible later developments.
2.Dynamic Lorentz Forces
3.Signal Modulation and Field Strengths
4.Thermal Velocities and Plasma Density
5.Measurement Examples
6. Increased Plasma Densities
7. Partly and Fully Ionized Ions
8. Fusion Temperatures
9. Conclusion
10. References
Introduction
As noted in some other publications the magnetic field oscillation
amplified thruster MOA [1, 6] originally was designed as flexible
low thruster with the ability reaching also a high ISp for deep
space missions and also in NSSK applications capable to use any
fuel that can be transformed in a gas [2, 9].
A main component of a MOA device is a coil system to generate
an altering magnetic confinement and a magnetic nozzle. Hereby
the shape of a primary magnetic field will be periodically altered
by the interaction with a secondary magnetic field. Therefore the
primary coil is permanently DC supported while the also DC supported
secondary coil is periodically modulated [3, 4, 7]. At the
moment the system was tested with several devices in frequencies
between 1 Hz and 3 MHz at field strengths between 130 mT to
1 T.
The pre-ionized fuel will be heated in a way that is similar to effects
in the magnetosphere of our sun and also other stars. In the
plasma densities of a usual mass flow of a low thruster [10, 11]
with a nearly full degree of ionization the ion gas temperatures is
reaching up to 10.000° K. In less plasma densities the energy fed
into the system by the heating mechanism will be distributed to a
much less number of ions increasing their kinetic energy and so
their temperature. Hereby also the plasma sonic velocity inside
the magnetic confinement will be altered affecting the exhaust
velocity of a thruster. Some of these settings also could be in
interest for a thruster running in a high ISp mode with low thrust
density [5, 8].
Dynamic Lorentz Forces
Usually the interaction of a quasi-stationary charges particle in
defined by the Lorentz force sometimes also noted as classic J x
B force.
F = e . v . B . sin(ß)
where v represents the velocity of the particle which moves in a
spiral like trajectory with the mean gyration radius.
r = m . v / (e . B)
while v as a thermal velocity depends on the temperature. These
classic J x B force is less significant in the heating mechanism of a
MOA device rather than in a MPD device for example.
In an environment dominated by altering magnetic field strengths v must be replaced by vA based on a magneto acoustic phase velocity
oversimplified described by
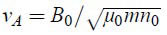
while v as an average radial velocity of the ions spiral trajectories
with the radius r averaged towards and away from the gradient
equals zero relative to the vector of the magneto acoustic wave in
the z axis of their movement
rz = r - r
vz = v - v
Therefore the charged particles in the plasma remain quasi static
in relation to any wave phenomena along the z axis in a magnetic
field. Of course they tend to spiral towards the fields gradient because
r is smaller in the direction towards the gradient where the
local field strength is a little bit stronger. Due to this slow accumulation
the density of charged particles usually is slightly increasing
along the gradient in a static magnetic field. But this movement is
not significant against a high value of vA.
Looking at the definition of the Lorentz force so v is to replace by
vA in case of an interaction with a magneto acoustic wave along
the z axis.
F = e . vA . B . sin(ß)
It does not matter which inertial system is moving, the consequence
remains the same. The transfer of energy therefore depends
on the values of vA and dB where
dB = B0 - B(x, y, z)
in respect to the local value of B at the particles location before
interacting with the wave phenomenon.
Therefore is to differentiate between a classic Lorentz force and
a dynamic Lorentz force in the environment of altering magnetic
fields.
Signal Modulation and Field Strengths
In a classic AC modulated coil the strength of the magnetic field
is increasing between zero and maximum depending to a sinus
function. Therefore the velocity vA of any magneto acoustic wave
depending on B0 is increasing in the same manner and reaches its
maximum value only for a short asymptotic small time. Hereby
the energy transfer via a dynamic Lorentz force depending on vA
and dB is not really significant.
Thus this effect becomes more significant in the magnetic field
of DC supported coil which periodically changes its shape due to
interaction with the magnetic field of secondary dynamic modulated
coil. This is the principle of the MOA device claimed in an
earlier patent AT502984 (A1) by the author [13].
Of course also in this two coil configuration the signal response
time also depends on the electro-technical parameters of the
secondary coil but the field strength B0 at the gradient of the
primary field and therefore also vA is always is at its maximum
during the full cycle.
Despite this dB depends on the shape of the magnetic field and
therefore on the construction of the coils as a topic in the development
of MOA. Hereby the design of the new MOA P5-typecoils
and their modulation is to note but not to discuss in detail
at the moment.
Thermal Velocities and Plasma Density
As seen in the simplified formula defining the velocity vA of a
magneto acoustic wave, its value also is depending on the plasma
density.
![]()
Although there are several variations of this formula at least it depends
on the relation between the mass of charged matter and the
number of charges in a defined volume. So in a low dense plasma
the energy will be distributed only to less particles via a stronger
dynamic Lorentz force due to a higher vA resulting in increased
thermal velocities. Similar conditions can also be found in a partial
ionized gas with very low density. Because the charges particles
are coupled by their charge a plasma behaves like a fluid even if
the mean free path is greater than the diameter of the confinement.
In this condition the neutral gas will not be disturbed by the
plasma even if the pressure of the plasma is increased due to its
temperature.
In several measurements MOA has generated a kinetic ion energy
of 11 keV. Hereby this result was measured the first time with
a mass flow of 50 sccm aka 1 mg/s Nitrogen with a degree of
ionization of 2% at a gas pressure of 10-4 mbar in the vacuum
chamber with a free mean path of 6,2 m in the gas. This result was
reproduced with different mass flows and therefore gas pressures
but with the same power in the pre-ionization device. Finally with
an improved pre-ionization device with an increased degree of
ionization to generate more thrust also the kinetic ion energy decreased.
The energy transferred by the dynamic Lorentz force onto the
Nitrogen ions has a value of 1,06 . 10-14 J per particle resulting
in a thermal velocity of 9,56 . 105 m/s according to an ion sonic
velocity vi of 2,76 . 105 m/s according the definition of the Bohm
velocity
vi² = k . T / m
Using the Langmuir approximation to respect the electron gas
temperature
vS² = vi² . [1 + (Te / Ti)]
the resulting plasma sonic velocity vS has a value of 3,9 . 105 m/s.
So the kinetic energy of the ion has the value of 1,77 . 10-15 J according
to 11 keV.
Thus in this example the ions are singl ionized therefore Te and Ti
have the same value if the electron gas is not disturbed by external
excitation [15-17].
Measurement Examples
In the low dense environment there are no laminar effects and
the plasma does not interact with the remaining neutral gas in the
confinement because of its free mean path. So the exhaust velocity
of the plasma plume guided by the magnetic nozzle only depends
on the plasma sonic velocity vS. By impacting into a defined
target the kinetic energy of the ions can be calculated by measuring
their impact depth. A useful tool for the calculation of these
stopping range tables for example the SRIM tool by James Ziegler
[14] applying the well known Bethe-Bloch equation.
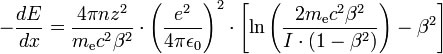
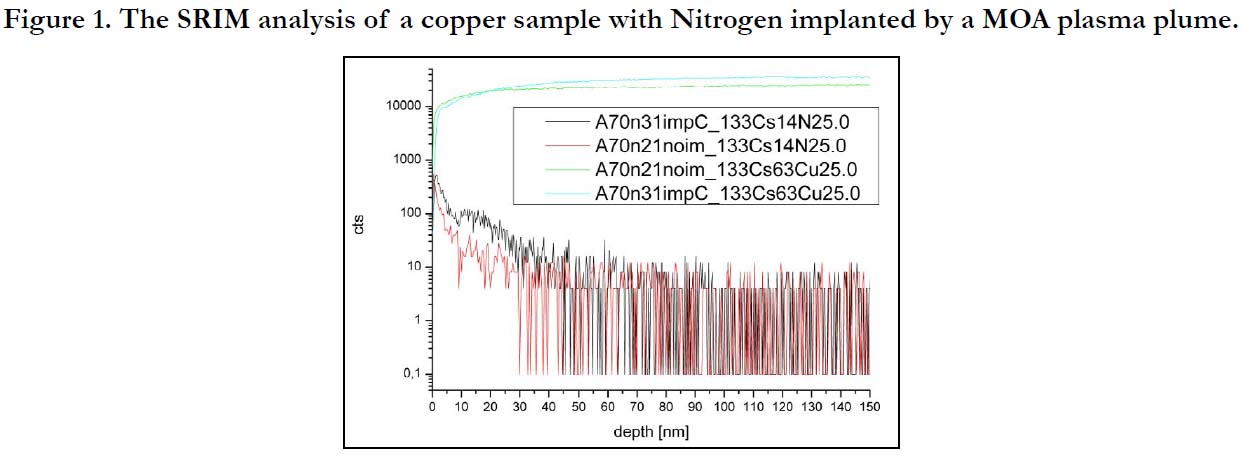
In the measurement examples discussed hereby copper samples
were used as targets analyzed at the University of Augsburg [12].
Hereby the maximum of counts of N-signals was detected in a
depth of 13 nm according to a kinetic energy of 11 keV.
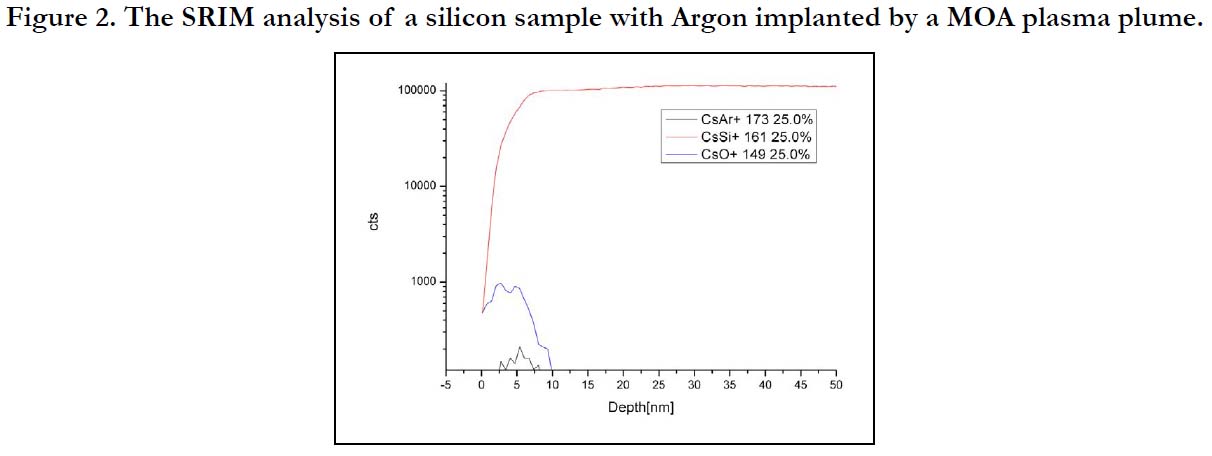
Comparing measurements were performed by the use of Silicon
targets proceeded with Argon ions. Hereby the maximum of implanted
Argon was detected in a depth of 6 nm also according
to a kinetic energy of 11 keV. The kinetic energy in the value of
1,06. 10-14 J per particle transferred by the dynamic Lorentz force
onto the Argon ions corresponds to a resulting thermal velocity
of 5,66 . 105 m/s of the Argon ions according to an ion sonic
velocity vi of 1,63 . 105 m/s and a plasma sonic velocity of 2,31.
105 m/s according to a kinetic impact energy of the plasma plume
in the value of 11 keV.
Similar measurements were performed by implanting Nitrogen into Aluminum samples in other test
series analyzed for example by Fraunhofer IGB in Stuttgart. So the 11 keV mark became a calibration
point for several settings on MOA devices. This also was done as an additional measurement of the
exhaust velocities by performing thrust measurements with low plasma densities.
Increased Plasma Densities
In an environment of increased gas pressure the plasma begins to
interact with the neutral gas distributing the thermal energy into
the neutral gas affecting v according to
v < vA . (mi . n / m . n)
in an advantage to generate thrust. Hereby m describes the mass
of neutral gas particles.
Therefore a low pressure environment with a low plasma density
is necessary to generate high temperature ions which are topic in
this discussion [11].
Partly and Fully Ionized Ions
In these examples noted above the ions in the plasma were single
ionized with only one electron left the orbit. In respect to the
mass of the power source of a spacecraft the ion gas in a plasma
should only be single ionized. Not only the pre-ionization device
but also the beam power of a thruster must be supported by onboard
systems [10, 11]. But also the different conditions in a plasma
depending on multiple or fully ionized ions should be noted in
the further discussion.
Because of their rest mass the thermal velocity of the ions in
a plasma is lower than those of the free electrons at the same
temperature. In the condition of a plasma containing multiple or
fully ionized ions these balance is shifted [11].
Regarding again the definition of the Lorentz force so is to note
that e as the elementary charge is to multiply with the number of
charges in the nucleus of an ion which are not compensated by
remaining electrons it its shell
F = Zi . e . vA . B . sin(ß)
where Zi is the difference between the Atomic number and the
remaining electrons in the shell of the ion.
Therefore the energy transferred to a multiple or fully ionized
ion accordingly has a higher value than which is transferred to
an electron with only a single charge. So the ion gas temperature
becomes greater than the electron gas temperature. Although because
of the mass of the ions the thermal velocity of the ions
remains less than that of the electrons. But this fact should be
respected in the intension to heat up ions in a plasma. This finally
also results in an increased plasma sonic velocity and so in an increased
ISp in the application for a thruster. Because of the need
to support the beam power by the mass of an integrated power
supply this option should be well calculated but in other applications
it could be an advance in any case.
Due to the strength of the coupling forces between the nucleus
and the ions remaining electron shell and because the accelerated
nucleus distributes the energy to a number of remaining electrons
it must not lead to a multiple ionization in a plasma heating by
Lorentz forces by itself. Therefore scattering processes are still
the dominant factor for multiple ionization of ions in a heated
plasma. So in a low dense plasma with a long free mean path
inside a small confinement also the degree of multiple ionization
remains low. This also is consistent with the conditions of the measurement examples noted before. Of course a higher degree
of pre-ionization leads to increasing secondary ionization processes.
Finally a multiple or fully ionization of the ions in a plasma
depends on the distribution of temperature the whole confined
mass also including the originally not pre-ionized gas. Hereby is to
refer on the brief note above respecting increased plasma densities.
Fusion Temperatures
Kinetic energies above 10 keV are applied in some fusion devices
in mainly homogenous confinements. Beside the long term stability
of magnetic confinement hereby the reaction rate is the main
issue to reach a positive energ balance. Maybe a contracting confinement
generating dynamic Lorentz forces could be an idea for
further discussion because the stability of the confinement would
not be an issue hereby. Up-scaling a MOA-like device possibly
adapting on a larger and maybe torodial confinement to enable
sufficient reaction rates therefore would be the challenge.
Additionally is to note that a real clean and possible economic feasible
fusion technique could use aneutronic reactions like 11B + p
or 7Li + p with the final product of 4He. The efforts to generate
3H or 3He had to become more economic than the production
of isotopes used in fission processes. In example the necessary
ion temperatures to use the resonance of the 11B nucleus at 660
keV would be a challenge for itself especially to adapt a thruster
device.Although it is a logical step for any technique to realize
fusion processes using De with 3H or 3He with least necessary
energies at first the 10 keV value is to discuss [18, 19].
Maybe the principle of MOA could be an idea for the efficiency
of plasma heating it is not a solution for the issue to generate sufficient
reaction rates in the existing design at least at the moment.
Conclusion
Because of the relevant kinetic energy of the ions in some settings
it was frequently asked if MOA could be used as a fusion
device. The answer is simply that it is not designed to generate a
reaction rate to enable a positive energy balance as seen in this
brief overview.
The fact that its mechanism enabling the use of dynamic Lorentz
force is in need to lesser energy input to generate relevant temperatures
than some other techniques could possibly offer some
discussion on thinkable options to use its principle in this view in the future. At the moment the development is focused on other
applications that can use this technology generating high plasma
temperatures and of course also in its origin application as an effective
electrically supported thruster.
References
-
[1]. International Astronautical Federation (IAF) [Internet]. France: International
Astronautical Congress (IAC); 2023. Available from: https://
dl.iafastro.directory/search/?q=hettmer
[2]. Frischauf N, Hettmer M, Grassauer A, Bartusch T, Koudelka PO. MOA: Magnetic Field Oscillating Amplified Thruster. In56th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law; 2005. p. C4-6.
[3]. Frischauf N, Hettmer M, Grassauer A, Bartusch T, Koudelka O. Recent developments of the MOA thruster, a high performance plasma accelerator for nuclear power and propulsion applications.InProceedings of the 2008 International Congress on Advances in Nuclear Power Plants-ICAPP'08 2008.
[4]. Frischauf N, Hettmer M, Grassauer A, Bartusch T, Koudelka O. Recent Achievements in the Development of the MOA Thruster, a high Performance Plasma Accelerator for Space and terrestrial Applications.InProceedings of the IAC 2009 congress, 60th International Astronautical Congress (IAC).Republic of Korea; 2009.
[5]. Frischauf N, Hettmer M, Koudelka O, Löb H. MOA2—an R&D paradigm buster enabling space propulsion by commercial applications. InProceedings of the IAC 2010 Congress, 61st International Astronautical Congress (IAC).Czech Republic; 2010.
[6]. Acta Astronautica: https://www.sciencedirect.com/ search?qs=manfred%20hettmer
[7]. Frischauf N, Hettmer M, Grassauer A, Bartusch T, Koudelka O. Recent activities in the development of the MOA thruster.ActaAstronautica. 2008 Jul 1;63(1-4):389-99.
[8]. Frischauf N, Hettmer M, Koudelka O, Löb H. MOA2—an R&D paradigm buster enabling space propulsion by commercial applications. ActaAstronautica. 2012 Apr 1;73:173-82.
[9]. New Technology: Austrian Plasma Propulsion. M.Hettmer, Raumfahrt- Concret 2/2006
[10]. Löb H. Nuclear engineering for satellites and rockets.Thiemig; 1970.
[11]. Ionenraketen H.Löb, J.Freisinger - Vieweg&Teubner, Wiesbaden 1967, ISBN 978-3-663-06352-0.
[12]. Untersuchung von Implantierten Cu-Proben, Universität Augsburg, Bericht 3870 660.
[13]. Espacenet- Austrian Patent Office:
[14]. Ziegler JF. SRIM (the stopping and range of ions in matter) software.
[15]. Zohm H. Plasmaphysik I. In LMU Munich (WS 2012/2013) 2012.
[16]. Nishikawa K, Wakatani M, Wakatani M. Plasma physics. Springer Verlag; 1990.
[17]. Spatschek KH. TheoretischePlasmaphysik: EineEinführung. Springer-Verlag; 1990.
[18]. Duderstadt JJ, Moses GA. Inertial confinement fusion. John Wiley & Sons; 1982.
[19]. Ruggiero AG. Nuclear fusion of protons with boron. Brookhaven National Lab. Upton, NY (United States); 1992 Sep 1.