Numerical Simulation of a Bat Wing at a Wing Beat
Amelian M1, Sharifi F2*, Baghernejad A2
1 Department of Aerospace, Sharif University of Technology, Iran.
2 Department of Aerospace, Garmsar Islamic Azad University, Iran.
*Corresponding Author
Farzad Sharifi,
Department of Aerospace, Garmsar Islamic Azad University, Iran.
Email: sharififafa@gmail.com
Received: May 04, 2019; Accepted: August 26, 2019; Published: August 28, 2019
Citation:Amelian M, Sharifi F, Baghernejad A. Numerical Simulation of a Bat Wing at a Wing Beat. Int J Aeronautics Aerospace Res. 2019;6(4):200-204. doi: dx.doi.org/10.19070/2470-4415-1900024
Copyright: Sharifi F© 2019. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
Abstract
The purpose of this research is to model the bat's Arfoil in a Wingbeat and study the flow behavior around it. There are different species of bats living in nature. In this project, Because of the wide range of bats, 12 bat species have been Selected and their dimensions and characteristics have been averaged and used as reference dimensions, In order to obtain the velocity and how to flap a wing, a bat species have been studied at different speeds. The maximum flight speed has been selected for the analyzation and the way of the movement of the wing and the amplitude of the oscillation at this speed was estimated using experimental data. After estimating of the wing movement, the frequency and amplitude of each wing airfoil can be obtained. The air flow through the middle airfoil in the movement of the bat wing was modeled by using the numerical simulation of the fluid and the coefficients of lift and thrust were calculated for the airfoil. At the end, the flow separation was simulated in the motion of the flap and the structure of the flow around the airfoil was investigated.
2.Introduction
2.1 History of studies on birds and bat’s flight
2.2 The Strouhal number
3.The Dimensions of Airfoil of a Bat’s Wing
4.Wing Beat Frequency and Amplitude
5.Numerical Simulations
6.Discussion and Analysis of Results
7.References
Keywords
Bat’s Airfoil; Numerical Simulation; Pitching; Plunging.
Introduction
The inspiration from nature, firstly used by leonardo davinci the famous artist, which later led to the foundation of the science of bionics. He inspired bat’s wing that could be seen in his drawing for design of flying machine, he had chosen the structure of a bat’s wing for his aerial vehicle structure, and he intended to simulate the movement of the flywheel with a cloth reinforced by wooden beams. After it, a lot of research has been done to understand how the animals fly to inspire the design of new aircrafts.
Understanding how a bat flies, helps us to inspire new idea for designing new vehicles. The aerodynamics of the flying bat are very complex because there is not a constant Lift nor a thrust force; Both of these forces are generated in a close cycle due to the flapping of the wing at all times. Each part of the body of a bat has various anatomical characteristics that affect the aerodynamics of flight, such as lift and drag. We focus on relatively newer work that to change the ways in which we understand how bats carry out their remarkable flight behavior, and that the way we understand the structural underpinnings of bat flight. In this paper, we provide an overview of the morphology of bats from the perspective of their unique capacity for powered flight. Throughout the paper we provide references to classic literature concerning animal flight and the bat flight apparatus, and direct readers to sources of additional information where possible. These include lift and drag forces, unsteady effects and Strouhal number.
A lot of research has been done on the flight of birds and how to create up and down forces with their wings. These studies included the building of aerodynamic models and testing them in a wind tunnel [1, 2]. The calculation of the pitching airfoil that produce lift force, like the wing of birds is one of the topics that scientists have been interested in., The Thrust force generation and propulsion efficiency in plunging and pitching of the airfoil were studied, in these studies, the wing movements were assumed to be harmonic during the flight [3]. Also, numerical simulations have been used to obtain the airfoil lift, and thrust force, in these analyses, the effects of viscosity and separation were considered [4].
Some researches focused on aerodynamics of bats and its flight. These researches measured the speed of the bat wingbeat in a wind tunnel, and showed patterns of airflow around the wings and its wakes [5]. In other research, scientists installed sensors on bat wings that indicate how The bat flapped in maneuvering mode and direct flight [6]. For the modeling of the bat wing experimentally, a flexible plate was used and the frequency of flapping was applied And aerodynamic forces were measured [7].
\
Strouhal number is a dimensionless parameter that describes the oscillating flow mechanism and can predict flow unsteadiness. This number is used to govern a well-defined series of vortex growth and shedding regimes for airfoils undergoing pitching and heaving motions [8, 9]. The Strouhal number is often given as equation 1,
St = fL/U, (1)
Where f is the wing beat frequency, L is peak-to-peak oscillation amplitude and U are the flow velocity.
The region of favorable force production peaks within the interval 0.2<St<0.4, and outside this region unsteadiness of the flow may become crucial. Cruising flying animal converge at a narrow range of St corresponding to a regime of vortex growth and shedding in which the propulsive efficiency of flapping wings peaks [10].
The Dimensions of Airfoil of a Bat’s Wing
Bats are the only mammal that can fly. The wings of the bat are different from the wings of the birds and are made differently, but instead, the woolen skin of the bat is similar To leather and has an elasticity that causes its wings to be Drawn along the bones that move the hands and fingers off the bat. The wing beat of the bat is not like birds that wings all up and down, they completely open their fingers [3].
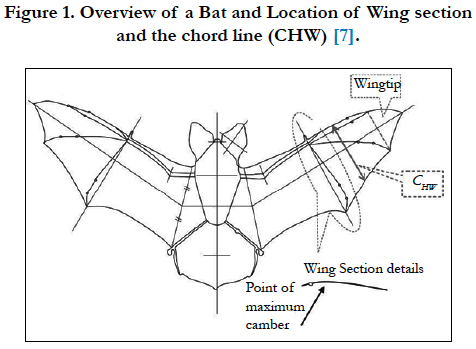
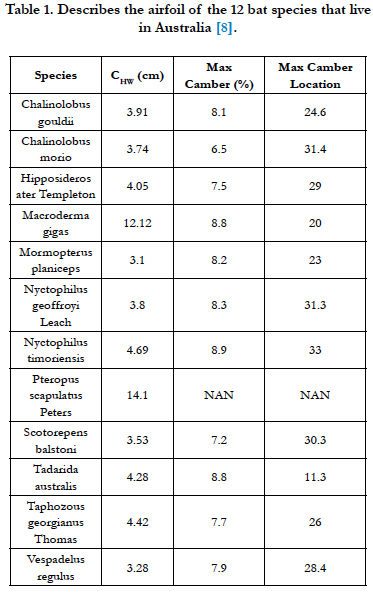
To analyze the wings of a bat we require detailed information on the dimensions and shape of the bat’s wings. There is 1240 species of bats in nature and bats make up about 20% of mammalian species. So for analysis, we need the information of some species. Table 1 shows the description of the airfoil of the 12 bat species that live in Australia that we can use it for analysis. The location of airfoil that described in table 1 is shown in figure 1, the location of this airfoil is 30% wing from the wing tip and CHW is chording of this airfoil.
We need to select data from table 1 to generate an airfoil to a simulate wing beat flow. The selected data must be close to 12 bat species characteristics, thus the selected airfoil chord is 4 cm and the maximum camber is 8% and its location is 25% of chord line. Equation 2 has been used to produce this airfoil.
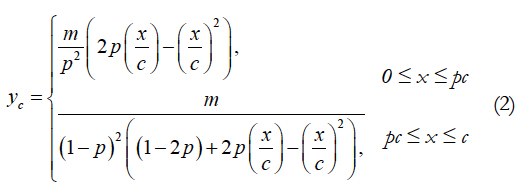
In this case, m is the maximum size of the chord relative to the chord and p its location. Therefore, m = 0.08 and p = 0.25. After applying these numbers in the equation, Airfoil is as follows:
Wing Beat Frequency and Amplitude
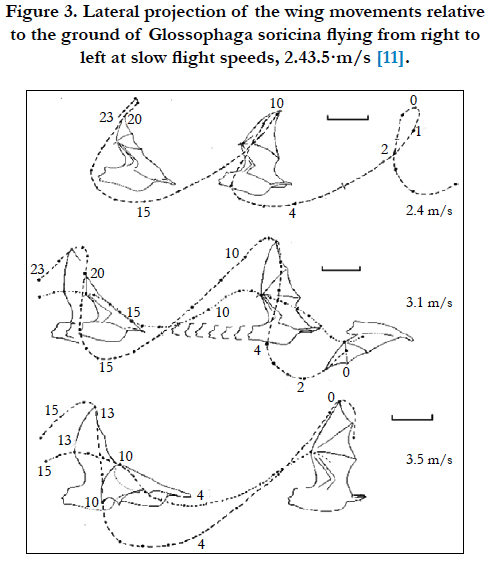
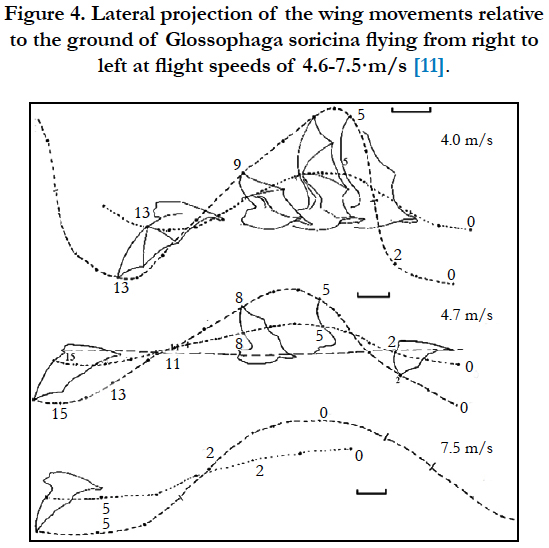
The flapping of the bat’s wing is different in various flight conditions. So, Norberg examined a specific species of bat called Glossophaga Soricina, a native of the Americas to detect various kinds of bat wing flappings [3]. He examined Glossophaga Soricina in a 30-meter long flying tunnel at different flight speeds. He saw that when a bat is hovering and flying at low speeds, the tip of the wing moved opposite the direction of the wing to create force. This backward movement vanished from a speed of flight at 3.2 m/s and over it, so the direction of movement of the tip of the wings will be same direction of wing beat at these speeds. The strouhal number also decreases with increasing flight speed at speeds greater than 4 m/s, this number is <St <0.22. According to the definition and limits mentioned in the previous section, at this speed the effects of unsteadiness decreases and forces that produce will be optimized.
According to measurements made by Norberg at different flight speeds, he obtains relationships for the calculation of the frequency (equation 3) and the strouhal number in terms of velocity (equation 4).
f = 14.8 V-0.277 (3)
St = 1.93 V-1.37 (4)
Norberg showed the kinds of wing beats in various bat flight speeds, his drawing is shown in numeric 4 and 5. As seen in these Figs. When the speed of the bat is increasing the frequency of the flap is reducing. According to these Figs. The direction of the tip of bat’s wings is not going back when flight is increased. We select the highest speed of the flight of bats to analyze airfoil, because in this strouhal number has less unsteadiness effects and it has higher lift and thrust efficiency. Therefore, for analyzing, the flow rate is 7.5 m/s and the wing beat frequency is 7.8 Hz.
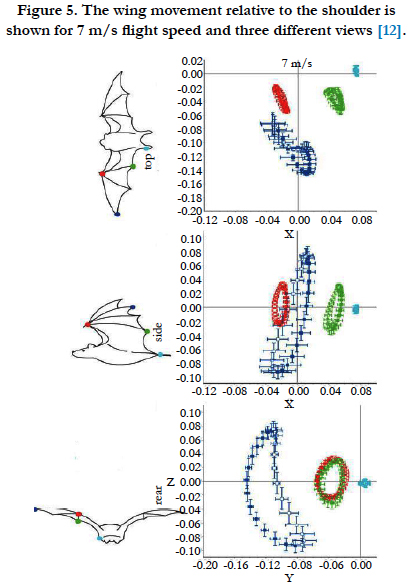
To obtain the amount of displacement of airfoil in a wing Beat, we extract data from Busse experiments [12]. In Busse’s experiment's data, the multi-point motion chart on the bat's wing is shown in three main pages, which can be used to determine the amplitude of the oscillation of each point. This data for speed of 7 m/s is very close to our selected flight speed.
Figure 3. Lateral projection of the wing movements relative to the ground of Glossophaga soricina flying from right to left at slow flight speeds, 2.43.5·m/s [11].
Figure 4. Lateral projection of the wing movements relative to the ground of Glossophaga soricina flying from right to left at flight speeds of 4.6-7.5·m/s [11].
As shown in Figure. 5 the in yz plane, the two green and red points are approximately the same domain. The motion of this point is three-dimensional, the displacement of the wing is higher in the z direction and the velocity of the bat is in the x direction, so we should use xz plane for the two- dimensional analysis. From the xz plan data, we can extract the values of the airfoil oscillation such as percentage amplitude to chord line, the minimum and maximum angle of attack. So the amplitude of the oscillation is 0.85, the maximum angle of attack is 7.6 and minimum 3.4 degree.
Figure 5. The wing movement relative to the shoulder is shown for 7 m/s flight speed and three different views [12].
Numerical Simulations
For numerical modeling of the airfoil, first we assumed the airfoil of the bat is fixed (at the average of the wing beat angle of attack 5.5 degrees) and the flow speed is 7.5 m/s. Also, Reynolds number calculated with flow speed and value is 2×104, so the flow through the airfoil is laminar. After doing simulations, we calculate the coefficient of lift and drag. The method was used for simulation is simple, that is pressure-based method and the equations discretized second order.
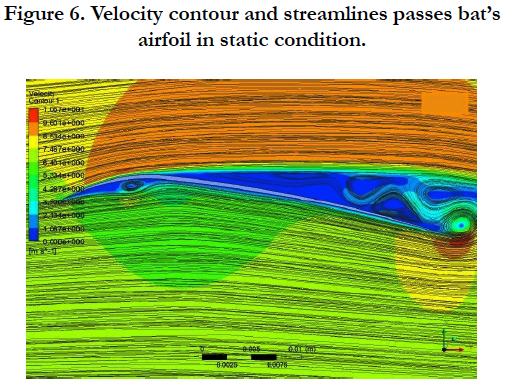
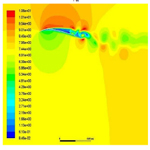
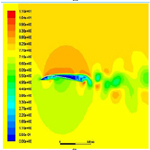
Velocity contours and streamlines in the static condition after simulation are shown in Figure 6. As it is shown in this figure, the flow is separated from the beginning and forms a vortex at the lower surface of the airfoil, this vortex is static and has constant strength. This vortex causes the flow to pass through the lower surface of the airfoil, like it passes a thick airfoil. On the upper surface of the airfoil, the flow is separated from the 1/4 chord and forms vortices. These vortices begin to move, which causes oscillation in the drag and lift forces. Table 2 shows lift and drag coefficient of wing airfoil, these values have a max and min because the flow over an airfoil separated and fluctuating.
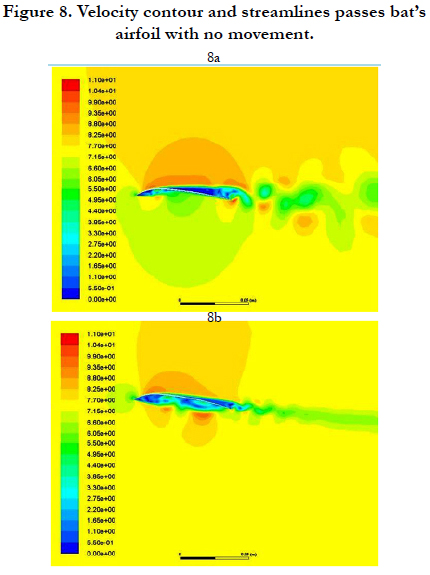
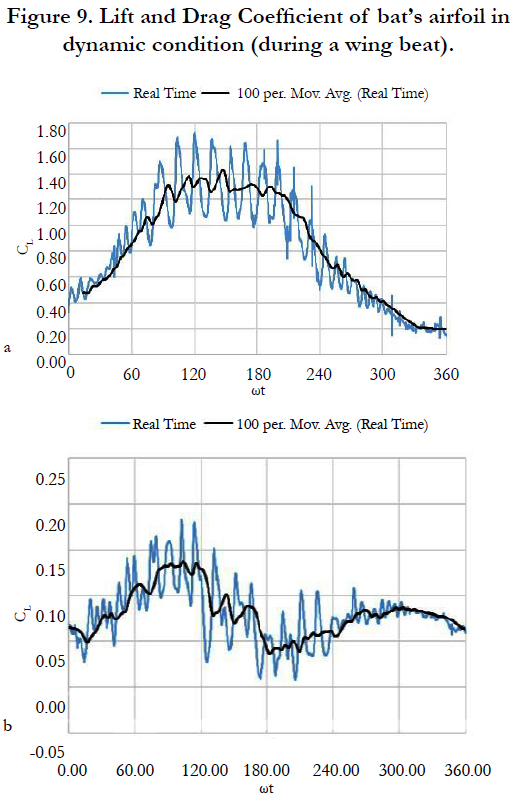
For dynamical analysis (wing beat), the frequency, amplitude and angle of oscillation used extracted data are used. We simulate several full-period of bats flapping and the results are averaged in time. Velocity contours and the separation points show in Figures 7 and 8, in these figures the position airfoil during a wing beat is shown: up, middle (up to down), down and middle (bottom to top). The coefficient of lift and thrust of the airfoil in a complete wing beats. The period is given in Figure 9.
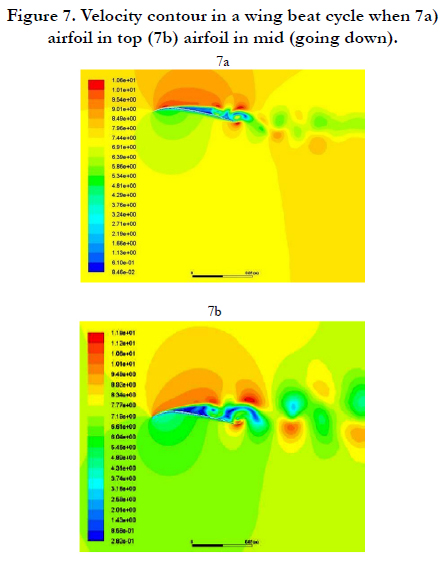
Figure 7. Velocity contour in a wing beat cycle when 7a) airfoil in top (7b) airfoil in mid (going down).
Discussion and Analysis of Results
The distribution of the flow around the airfoil can be seen in Figures 7 and 8. With seeing these figures we can find separation at the upper surface of the airfoil in all four states (7a, 7b, 8a and 8b), which causes making strong vortex in airfoil wakes. This separation and the Vortex are unstable and causes an intense oscillation in the forces, as Figure 9 shows, in addition, this separation creates a big low pressure area that causes extra drag add to airfoil drag. When the wing going down this separation area becomes bigger, this causes fluctuations more severe when the wings fall down. At the lower surface of the airfoil: when wing rising a separation region and a vortex forming such as in the static condition exist, which makes the flow pass the airfoil, looks like a thick airfoil. But at the lower surface of the airfoil the separation will be eliminated, which will help to generate a lift force. As shown in Figure 9, the wing beat operation produces a thrust force and increases the lift force. How does the bat overcome this separation over the upper surface of the wings? The answer is that in the calculations the flow is laminar, but the flow on the wing of the bat is turbulence due to the presence of posts and looms on its skin and the flow will separate at a further point on the surface. The other thing is not to consider the bone that passes through the wings that will affect the airfoil's appearance, and this bone will cause the flow after it to have a separation, but it will again become attached to the surface, which cause a drag force decrease significantly.
References
- DeLaurier JD. An aerodynamic model for flapping-wing flight. The Aeronautical Journal. University of Toronto. Downsview. Ontario. Canada. 1993; 97(964):125-30.
- G. K. Taylor, R. L. Nudds, and A. L. R. Thomas, “Flying and Swimming Animals Cruise at a Strouhal Number Tuned for High Power Efficiency.” Nature. 2003 Oct 16;425(6959):707-11. PubMed PMID: 14562101.
- Garrick IE. Propulsion of a flapping and oscillating airfoil. 1936; 567.
- Ashraf MA. Numerical simulation of the flow over flapping airfoils in propulsion and power extraction regimes. University of New South Wales, Australian Defence Force Academy, School of Engineering and Information Technology. 2010.
- Sterbing-D'Angelo S, Chadha M, Chiu C, Falk B, Xian W, Barcelo J, et al. Bat wing sensors support flight control. Proceedings of the National Academy of Sciences. 2011; 108(27):11291-6.
- Song AJ. Aeromechanics of highly compliant structures: bat wings, compliant membranes and flexibly mounted flat plates, Brown University, USA. 2013.
- Bullen RD, McKenzie NL. Bat wing airfoil and planform structures relating to aerodynamic cleanliness. Australian Journal of Zoology. 2007 Oct 16;55(4):237-47.
- Anderson JM, Streitlien K, Barrett DS, Triantafyllou MS. Oscillating foils of high propulsive efficiency. Journal of Fluid Mechanics. 1998 Apr;360:41-72.
- Wang ZJ. Vortex shedding and frequency selection in flapping flight. Journal of Fluid Mechanics. 2000 May;410:323-41.
- GK. Taylor, RL. Nudds and ALR. Thomas. Flying and swimming at a Strouhal number tuned for high power efficiency. 2003; 425:707-711.
- UML. Norberg, Y. Winter. Wing beat kinematics of a nectar-feeding bat, Glossophaga soricina, flying at different flight Speeds and Strouhal numbers. The Journal of Experimental Biology. 2006: 209: 3887-3897.
- RV. Busse, A. Hedenstrom, Y. Winter and LC. Johansson. Kinematics and wing shape across flight speed in the bat, Lepto –Nycteris. Biology Open. 2012; 1226-1238.